Quote:
Originally Posted by Farren
Quote:
Originally Posted by Michali
Right, thanks Farren, I'm pretty familiar with the emergence concept. The purpose of the thread though, and what is most interesting about your post is what you mean here:
Quote:
Originally Posted by Farren
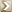
It depends on what the variables on both sides of the equation represent.
|
Can you help me understand what you mean by your use of "represent"? |
I mean we use numbers to represent, or quantify, qualities of things and collections of things. The speed of a bullet. The weight of an apple. The number of apples that exist. |
Right, ok, but are you sure you were talking about numbers when you made that statement? After all, you said it depends on what the "variables on both sides of the equation" represent. In a previous thread, we were able to describe an operation in a simulator as being expressible with "f(x)=y". Do you mean to draw a distinction between these or were those states essentially identical to numerical expressions as well?
Once again, what did you mean by 'f(x)=y is identical dependent upon what both sides of the equation are representing.'- paraphrased.
Quote:
|
Originally Posted by Farren
Quote:
|
Originally Posted by Michali
Quote:
Originally Posted by Farren
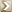
Mathematical equivalence does not imply shared material identity.
|
I agree fully here. "Material identity" is very interesting to me as it is the very thing I'm attempting to undermine. Is this "material identity" necessarily only useful for material examples or would you agree that your distinguishment is also the way we distinguish between "3+3" and "6"? |
Well I'm using material identity to mean the physical presence of the things that have the qualities we quantify. So the material identity of 4 apples is the apples themselves. Its possibly contentious to speak of the "material identity" of, say, the speed of a falling apple, but apples do indeed fall. We're describing something material, I think, when we talk about the speed of an apple. |
I think defining a thing as though it is separable from its qualities, you will find difficult. For instance, you consider the speed of an apple to be material, when it is actually a relative quality between you and the apple. Do you consider an apple's movement in a direction to be essential to the apple?
Quote:
|
So I think its fair to talk about the speed of two apples having different material identities. As in "the speed of one apple may be equal in value to the speed of another apple, but it is not the same physical property in the universe, even though it is in the same type of property". Certainly in all of our computations we treat them as seperate identities.
|
Can you not imagine the apple could have another speed? Of course one would think two different apples having the same speed are different. But what about one apple having a different speed? Suppose I throw it. Was not the apple that went through the air identical to the apple I once had in my hand? Also, what if my brother were bicycling next to it as it flew, and he watched it holding perfectly still when I watched it traveling quickly.
Quote:
|
They're different data points in the universe, different variables, even though they have the same value and describe the same quality of two different things.
|
So you say, given two apples, I have two different variables. If they are traveling at the same speed, they have a certain identical value called speed. That's fine of course, but in f(x)=y all the values on both sides of the equation are equal. Such as in the values expressed in 3+3=6.
If two apples had all the same values, aren't they the same variable? I mean, literally, every quality, including "point in space-time"?
Quote:
But could numbers themselves be considered to have similarly separate material identities?
I don't think thats a meaningful question, because we don't treat numbers as material things. They have mathematical identities. And whether functions of numbers have the same mathematical identity as numbers they yield is an interesting question.
In a previous thread I referred to lambda calculus, which is a formal system for describing all other mathematical functions and quantities, in the minimum possible set of symbols. Lambda calculus basically provides all the operations for a Universal Turing Machine (a theoretical universal computing device), which is the theoretical model for modern computers.
In any event, in lambda calculus, everything is reduced to the interaction of functions, even the mathematical identity of numbers themselves.
By its very nature, lambda calculus represents every number as a function of other numbers, as the following Church Numerals (numbers encoded in Lambda Calculus) demonstrate:
0 ≡ λf.λx. x
1 ≡ λf.λx. f x
2 ≡ λf.λx. f (f x)
3 ≡ λf.λx. f (f (f x))
...
n ≡ λf.λx. fn x
...
In other words, in this "underlying math of math", the identity of 3 is essentially a function of a function of 1.
So if we understand Lambda Calculus to describe the underpinnings of all math, then I'd say yes, the mathematical identity of (3+3) is 6 is (2+2+2). They're just different ways of writing down the same identity.
What are you angling at with this?
|
I mean to be angling that there is no need to distinguish f(x)=y as being identical from this concept of "yielding". And then to go from there. I tried looking up lambda calculus, and I'm super interested in it, and I'm hoping you can help me understand it. It reminds me of the set theory explanation for mathematics. First, what is the lambda symbol supposed to represent?